Trigonometri

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri



segitiga sikusiku

Dari gambar diatas kita dapat beberapa persamaan dari sudut alpha

SINUS ALPHA
sinus

COSINUS ALPHA
cosinus

TANGEN ALPHA
tangen

Dari Persamaan diatas dapat disimpulkan bahwa :
trigonometri sinus = DE-MI



cosinus = SA-MI



tangen = DE-SA


Yang dimaksud Depan, Miring, Samping adalah sisi-sisi segitiga berdasarkan letak sudut.
Dapat dilihat dari gambar segitiga diatas sin alpha adalah sisi di depan sudut alpha dibagi sisi miring segitiga.

Dalam Trigonometri ada sudut sudut istimewa yaitu sudut (derajat) 0, 30, 45, 60, 90
Tabel sin, cos, dan tan sudut istimewa


Data tabel diatas diambil/didapat dari segitiga dibawah ini :
segitiga trigonometrisegitiga trigonometri

Ayo kita buktikan
Kita akan membuktikan sinus 3o
sin 30
JADI sin 30

Terbukti kan ?
Sekarang silahkan sobat buktikan sin, cos, dan tan sudut sudut istimewa pada tabel. Apakah benar ??

Hubungan fungsi trigonometri

\sin^2 A + \cos^2 A = 1 \,
1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,
1 + \cot^2 A = \csc^2 A \,
\tan A = \frac{\sin A}{\cos A}\,

Penjumlahan

\sin (A + B) = \sin A \cos B + \cos A \sin B \,
\sin (A - B) = \sin A \cos B - \cos A \sin B \,
\cos (A + B) = \cos A \cos B - \sin A \sin B \,
\cos (A - B) = \cos A \cos B + \sin A \sin B \,
\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,
\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,

Rumus sudut rangkap dua

\sin 2A = 2 \sin A \cos A \,
\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,
\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,

Rumus sudut rangkap tiga

\sin 3A = 3 \sin A - 4 \sin^3 A \,
\cos 3A = 4 \cos^3 A - 3 \cos A \,

Rumus setengah sudut

\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,
\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,
\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,


Mungkin gak semua bagian di bahas, ini ada tambahan catatan" tentang trigonometri... bila ingin menambahkan boleh di komentar




Disini ada link download soal-soal dan pembahasannya
link download soal soal trigonometri dan pembahasa...
ini untuk soal-soal saja soal-soal trigonometri


bila ingin ditambahkan boleh komen..
Thx ^^


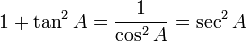
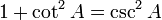
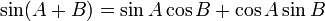
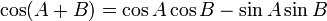
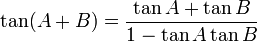
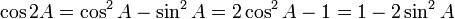
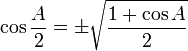
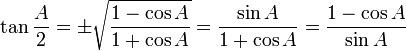
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Total